Concepto de contradominio en matemáticas

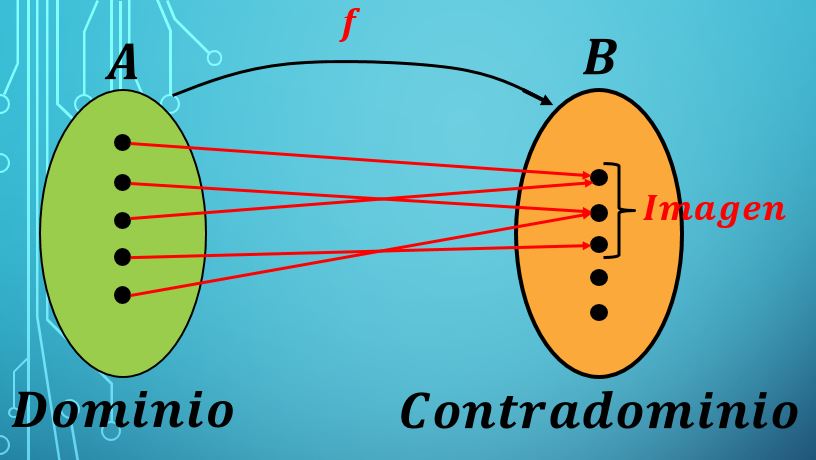
Si queremos dominar las matemáticas, es necesario que podamos tener en cuenta la definición de un conjunto de conceptos que son muy importantes. En este caso, hablamos del concepto de contradomino, el cual se refiere en términos de la función a aquel conjunto que cuenta con valores que podrían tomar la variable que es dependiente de la letra “y”. Por supuesto que también debes tener en cuenta que esta definición también es válida para los siguientes términos: el rango, el condominio y el recorrido.

Aunque es una definición que puede parecer muy sencilla, es necesario que se comprenda de buena manera ya que estamos hablando de variables y de dependientes que pueden alterarnos de forma completa algún ejercicio o problema que nos toque resolver con esos valores. Conoce más sobre la calculadora de factorizacion!

Concepto de contradominio en matemáticas

Recordando que la función tiene que ver con la unión o relación que viene dada entre los elementos de dos conjuntos, se puede decir que el contradominio de una función guarda su referencia hacia un conjunto de valores que tiene dependencia en la “y”. En este sentido, debeos tener en cuenta que hay varios valores o elementos que están en juego.

En sí, se habla del contrdominio, como un conjunto de elementos que son de llegada. También puede llegar a comprenderse como un conjunto final o un conjunto de condominio. Cualquiera de estas perspectivas son realmente válidas, solo que debemos tener presente cuál es la que estamos usando para no equivocarnos. Estos son conceptos que están más estrechamente vinculados al tema de las funciones ya que es uno de los objetivos que se estudian dentro de las matemáticas.

Otras definiciones de contradominio en matemáticas

Si partimos de la premisa de que una función es una especie de regla que establece una notoria correspondencia entre los elementos de dos conjuntos, podemos atrevernos a definir el contradominio como el conjunto de los números que son conocidos como reales. Puede definirse también como el conjunto de la función “f” o el conjunto de llegada. Básicamente, lo que vemos es la manera en la que los conjuntos parten y cómo llegan a algo ya establecido.

También se puede definir al contradominio como una contraparte a lo que habitualmente conocemos como dominio. Ya sabemos que ambos son fundamentales dentro de una función y en el estudio que podría sugerir la misma.

Datos sobre el contradominio en matemáticas

Si hablamos de una forma sencilla en relación a lo que es el contradominio, esto tiene que ver con la manera en la que se da una participación en la función. En el caso de una función que existe, podemos ver que el contradominio podría ser el conjunto de “y”; siendo este que no tiene nada que ver con el dominio propiamente dicho.

Básicamente, debemos estar atentos de los elementos que intervienen en cada uno de los conjuntos y de la naturaleza de la función para así poder distinguir de manera inmediata quién es contradominio y quién es el dominio de la función.